『萬尾亀折形』 「背子守(せこもり)」 ― 2010/03/01 22:27

背子守
甲羅より 籠れる手脚を 出で伸ばし 子守りの温もり 愛のメモリー
『千羽鶴折形』の、作品につけられた狂歌は、親子のようなかたちの『巣籠』でも、「襟もとへ顔をすこもり はづかしや けふ水あけと 祝ひ初てき」と、艶っぽいものになっていて、どうも苦手だ。と言いながら、愛のメモリーでもないと思うし(松崎しげるか!)、亀は変温動物のはずなので、温もりというのもどうかと思うが、狂歌があると、よりそれらしくなる。前出の「鳴子」と「八橋」も一首づつ詠んでみた。
鳴子
ナルコとは 眠りの病気と 聞くきみは 稲田を渡る 風も知らずか
八橋
オイラーは 七つの橋に 御明答 顰みに習ひて おいらは八橋
どうやら、わたしは、狂歌とはだじゃれであると思い込んでいる、というか、ネタのマニア度が上がりすぎている気が。
十球パズル ― 2010/03/02 23:48

先日、針金や立方体の木片とともに東急ハンズで買ってきた木の球で、同種のパズルをつくった。連結した2個の球×5で1辺3個の球になるの正四面体をつくるものである。
解答そのものは易しいが、じっさいに試してみて、摩擦の少ない面で安定させる解答というものがあることがわかった。鏡像を同じとすれば、原理的には解答はひとつなのだが、正四面体の4面がどれも同じになるわけではないので、安定させるには、どの面を下にするかが重要になる。なんでもじっさいにやってみると、発見があるものだ。
このパズルでは、結晶学でいう最密充填構造の「美しさ」が実感できる。このような積み方が、最密(最もぎっしり球を詰め込むことができる)であることは、ケプラーが予想したものだが、証明は400年後の1997年、T. C. ヘイルズ氏によってなされた。問題の設定から証明までの長さは、フェルマーの最終定理を超えている。
ラジオ出演 ― 2010/03/04 21:45

お笑いコンビのロザンさんによる、学生向けの教養番組で、内容は、拙著『本格折り紙√2』の話題を中心に、「身近な数字√2について楽しく学びたい」というもの。20分ぐらいだったが、あっという間で、「行って、録って、すぐ戻る」みたいな感じだった。
菅さんのボケが、わたしには「難しくて」、つっこめなかった。
写真は、台本にしてもらった、アナウンサーの加藤シルビアさん、ロザンの菅広文さん、宇治原史規さんのサイン。
『本格折り紙√2』誤植 ― 2010/03/04 21:47
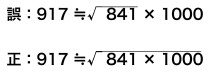
17ページ
「B判」説明
上図のように、√記号のかかる長さが短かすぎる。ということです。
トンデモ! 人生正四面体、あるいは風船説 ― 2010/03/05 22:11

話としてはもっともで、わたしも漠然と、そのことが、大人の時間が短い最大の要因と考えていた。しかし、これをじっさいに、横軸を年齢、縦軸を体感時間としてグラフ化(グラフ青:ゼロ近辺を扱いやすくするため、1/(t+1)として、その積分値をプロット)してみると、生物学的限界と思われる120歳を上限にして、全人生の半分が経過するのは約8歳ということになるのだった。これは、いくらなんでも実感にそぐわないのではないか。このグラフは、立ち上がりが急すぎるのだ。最近読んだ『大人の時間はなぜ短いのか』(一川誠著)という本でも、この説はおおざっぱなものだというふうに触れられていた。
ということを、さきに考えたわけではなく、話は、昨日、ひさびさに乗った満員電車で、時間しのぎで暗算をしたことから始まる。(わたしは、東京育ちなのに、電車通学、通勤の経験がなく、満員電車への耐性がたぶんひとより低い。本も読めないような状態だと、暗算や考えごとをしていないと、それこそ、時間がどんどん長くなってしまう。昨日はiPodのイヤフォンも忘れた)
このとき暗算したものに、球を正四面体状に積んださいの個数があった。数日前につくったパズルから連想したもので、「三角錐数」、「正四面体数」などというようだ。これから、気がついたことがあったのだ。その数列(0, 1, 4, 10, 20, 35, 56, 84, 120)が、乳児、幼児、少年、青年、中年、老人、そして生物学的限界というヒトの年齢モデルにかなりよく一致しているのじゃないか、ということである。
これを、さきほどプロットしてみた。
この正四面体の高さを、人生の体感時間とするわけである。年月を「下に向かって積んで」ゆくかたち、とも言える。生まれて1年で高さは全体の1/8になるが、次は1段増えるのに3年かかる。次は6年、10年となる。これが、緑のグラフである。これによると、体感人生の半分は二十歳である。そして、35歳が8分の5、還暦前が人生の4分の3である。これは、青いグラフのジャネーの法則より、ずっと実感に近いのではないか。しかも、人生の「節目」も示している。結論。人生は正四面体である。
なんて、ケプラーが、惑星軌道を内接する多面体で説明しようとしたようなトンデモ説である。だいたい、なんで、正四面体なのか、でまかせの説明もない。
で、ここで考えた。そもそも、体感時間がそれまでの時間に反比例するという説は、つまり、時間と経験(≒記憶)が比例するという説明であると言える。これを単純な比例でないとするとどうなるか。まっさきに思いついたのは、2/3乗(3乗根の二乗)ということだった。つまり、時間は風船がふくらむように体積として増えて行くが、それにしたがって、記憶・経験は、その表面積として増えるという仮説である。これは、、正四面体数によるグラフのきわめてよい近似になる(赤の線)。トンデモ説のわりには、なんだかもっともらしいぞ。
結論。時間は体積として蓄積し、人生はその表面に宿る。人生は風船でもあり、正四面体でもある。
トラックのマーク ― 2010/03/06 23:04

トコナメエプコスという、社名もちょっと不思議な会社で、遠目には、正三角形を、1:2:√3の三角形4つと、正方形に分割したかたちに見えた。
その場合、四つの三角形が合同になることはありえない。運転しながら暗算して、線の太さがないとすれば、分割の比率は、√3:2になると、とりあえず納得したが、面積にして3対4となる三角形が、一見して同じに見えるだろうか、分割線の太さを使った調整もあるのか、正方形と見えたが異なるのか、など疑問が残った。が、あとで作図してみる(図左)と、三角形は大きく違うようには見えないことがわかった。さらに、この比率の作図が、頂点を4等分することでできるということを発見した。(図右) これはなかなか美しい。
しかしである、さきほどネットで、この会社を検索して確認したところ、そのマークの、三角形と見えた図形のうちふたつが、台形になっているのだった。










最近のコメント