9ピースキューブ ― 2010/02/18 23:40

立方体を連結する方法は、面と面を合わせるだけではなく、辺と辺、点と点も考えられるので、三つの立方体の辺の連結パターンを数え上げたら、これが、ちょうど9種類になっていたのである。おおっと思いつつ、33の立方体がほんとうに組めるかという疑問があったが、これが可能であることが、いまわかった。前例がありそうな気もするが、これはよい。
このパズルをじっさいにモノでつくる場合は、辺と辺の連結部分を三角材で補強し、その他の辺は、その補強材のサイズで面取りをすれば、うまくいくと思う。
ベーゴマ ― 2010/02/20 00:16

このブログのタイトルの背景にも使っている、折鶴による風車というデザインにしたのだが、細い線がうまくでていないのは、ちょっと惜しい。でるはずと聞いていたのだけれど、単純な折鶴にしておけばよかったかも。
立方本(≠立方体) ― 2010/02/20 00:36

これを見ていて、そうか、正方形の本が三冊あれば立方体ができるのかと…。なにより、体という字と本という字が似ているので、立方体ならぬ、立方本というタイトルが、ツボにはいってしまった。あいにく、同じ大きさの正方形の本などないので、折り紙の本でつくってみた。
針金細工→九の図形→呪符 ― 2010/02/21 01:45
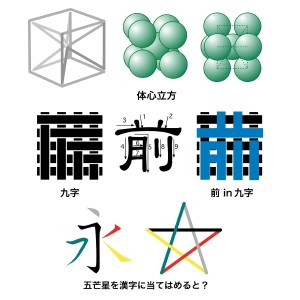
また、9と言えば「九字」があった。以前の書き込みでも触れたが、「前」という字は、九画であることから、九字も意味する。なお、九字「臨・兵・闘・者・皆・陣・列・在・前」の最後の文字も「前」である。
そして、そのときにも気がついたのだけれど、「前」の字は、単に九画であるだけではなく、九字の印の中に隠れている。
ここで、わたしの思考は、いつものようにずれてゆき、九字が「前」なら、九字と並ぶ護符である五芒星を漢字に当てはめると、なにになるかと考えはじめてしまった。
これは、「永」の字が相応しいということに決定。それぞれの筆運びを、陰陽五行の青(緑)・赤・白・玄(黒)・黄に対応させると、実にもっともらしい。「永」という字は「永字八法」で知られる特別な文字だし、いま思いついたわりには、ほんとうに昔からあった呪術のようである。
などと、今日も夜更かしをしているのだった。
キューブパズルの工作 ― 2010/02/22 23:22

このパズルに関して、キューブに関するパズルだけを集めた、秋山久義さんの『キューブパズル読本』や、世界的パズルデザイナーのStewart T. Coffinさんによる『The Puzzling World of Polyhedral Dissections』といった本などをあらてめて確認したが、前例はなかった。
(追記:2/25:と思ったら、なんという注意力散漫、『キューブパズル読本』に土橋創作さんのアイデアとして、掲載されていた。しかも、海外でプラスティック製で商品化されたとのこと。残念)
パーツ作製のルールがきれいなので、思いついたひとは他にいても不思議はない。そして、ソーマキューブと同程度に難しいという「よい問題」なのだが、製作の面倒さがネックになる。
(なお、『The Puzzling World of Polyhedral Dissections』という本は、 このサイトで全文が読める。久しぶりに本棚の奥から引っ張りだしたこの本には、1年前このブログで話題にした、古代ギリシアの「知恵の板」・ストマキオンのことも載っていた。忘れていたというより、通読していなかったということだ)
九点星のロウソク立て ― 2010/02/23 21:44

三角錐状の突起が、上下に三つずつ、四角錐状の突起が横に三つで、合わせて突起が九つとなる。中央はロウソクを立てるスペースで、下部も基本的には同じ構造になっている。
このかたちの基本になる立体として、図右上にあるような、三角形8個、四角形3個の立体が考えられる。しかし、この図面にはごまかしがあるのがわかるだろうか。三角形をすべて正三角形として、「側面」の「四辺形」の辺(稜)と辺(稜)のなす角度がすべて等しくなる場合を計算すると、それは約88.2度になる。直角ではないので正方形ではないわけだが、そもそも、正方形でなくても、あらゆる四角形の内角の和は360度である。これはどういうことか。
答えは、わかってしまえば簡単である。一般に、三本の線分を連結した図形は三角形になるが、四本の線分を連結した図形は、必ずしも平面図形である四角形にはならない。この4本の線分は、図右下の赤い線ように、菱形をかるく折ったようなかたちになっていて、平面図形ではない。
なお、この「十八辺体」は、針金の一筆書きでつくることができる。奇妙なかたちだが、五角形に見える角度があるので、五芒星を表現するのに向いている。











最近のコメント