ルービックキューブ ― 2008/10/19 10:11

『容疑者Xの献身』 ― 2008/10/21 00:49
さて。原作は、シリーズともども、出版されてすぐに読んだ。わたしは、ミステリを「気持ちよく騙されよう」ではなく「解こう」として読んでしまう癖(へき)があるので、仕掛けは早い段階でわかった。ストーリーテリングに感情をゆだねながらも、伏線を確認する読みかたである。よくできたミステリはネタが割れても面白い。そんな読みかたであっても、読み手は、作者の手のうちから大きくは外れていないし、外れようもない。そうした「作者と読み手」の相似形でもある「暗号と複号」「犯罪と捜査」に関連して、小説では、P≠NP予想が引き合いに出されていた。こうした数学ネタの衒学趣味が、この小説のひとつの味である。映画でも、それを示唆する台詞はあったが、P≠NP予想そのものへの言及はなかった。
一方、「探偵」が旧友の力を試す「パズル」として、いきなり、リーマン予想の反証なるものが登場する。原作もそうだったと記憶するが、あまりにネタがでかい。まあ、ちらりと台詞にでる、ホッジ予想とか、ヤン-ミルズ方程式と質量ギャップなど、有名なミレニアム問題は、呪文めいた名前ともあいまって、登場人物の天才性を強調する小説的・映画的ケレンになるので、演出の王道とは言える。
原作ではたしか、「数学はどこでもできる」という思想(あるいは幻想)を語るさいに、その象徴のひとつといえる、放浪の数学者・エルデシュの名があがっていたが、映画にこれがなかったのもちょっと残念だった。このほかに、「幾何とみせかけて関数」の台詞に、「位相幾何ではなく微分幾何」(ポアンカレ予想あらためポアンカレ定理の話:ミレニアム懸賞問題のひとつ)なんてのをかぶせれば、マニア(数学ファン)のウケはばっちりだったろう。
いずれにせよ、ミステリに登場する数学や物理、たとえば、モリアティー教授の二項定理(!)とか、『僧正殺人事件』の相対論などよりは、ずっとそれらしい。わたしも「それらしい」しかわからないけれど。そもそも「マニア(数学ファン)のウケ」ってなんだかわからないぞ…。小説と違って「地の文」のない映画は、ごちゃごちゃ説明できないので、難しい注文である。
作中で重要な定理(問題)は、四色定理である。これは、「なんだか難しそう」ということだけでは終わっておらず、「隣りと同じ色になってはいけない」という登場人物の孤独を象徴する演出の小道具になっていて、なかなかのアイデアだった。
未解決問題ということなら、ゴールドバッハ予想なんかはどうだろう。
「2より大きい偶数は2つの素数の和で表すことができる」
四色定理と同じく、問題の意味がわかりやすいぶん、詩や隠喩を感じることができる。雰囲気が『博士の愛した数式』になってしまうところがあり、映像的でもないが、これを使ったシーンを、想像してしてみた。
内海刑事「あの式は何ですか」
湯川「ゴールドバッハ予想を扱っていたのだろう。素数に関する未解決問題だ」
…(素数の説明)
内海刑事「つまり、素数って孤独な数ということですね」
湯川「面白いことを言うね。2より大きい偶数は2つの素数の和で表せるんだ。それが、ゴールドバッハ予想だ。予想ということは、証明はされていないということだよ」
内海刑事「素数と素数が結ばれるという話ですか」
ベタである。
なお、ゴールドバッハの予想をネタにしたものに、『ペトロス伯父と「ゴールドバッハの予想」』(アポストロス-ドキアディス著 酒井武志訳)という素晴らしい小説がすでにある。
危の中の螺旋 ― 2008/10/22 20:50

今年のノーベル文学賞はル・クレジオ氏だったが、20年以上前、たしか『数』という題名の小説を読んだぞと思い、探してみた。『数』の著者は、フィリップ・ソレルス氏(岩崎力訳)だった。いま手元にないが、たしか、漢字を使ったタイポグラフィー的な実験をしている小説で、それが翻訳されているので、さらにややこしいことになっていたはずだ。
タイポグラフィーから、文字に関するジャメビュ感覚に連想が飛んだ。見なれた文字が奇妙なものに見える心理現象である。この連想には、ちょうどいま、『プルーストとイカ-読書は脳をどのように変えるのか? 』(メアリアン・ウルフ著、小松淳子訳)という、読字障害のことを中心にして、文字を読むことに関する脳科学の知見を書いた本を読んでいるのも関係している。同書には、こんな引用もあった。
Yの字のなんと絵のように美しいことか。なんと無限の意味を秘めていることか、あなたは気付いているだろうか? その木もY、二本の道がぶつかる所もY、注ぎあう二本の川、ロバの頭と雄牛の頭、脚付のグラス、茎の上に咲き誇るユリの花、両腕を差し伸べる物乞い、どれもYだ。人間が考えだした文字の要素を成している万物に、同じことが言える。(ヴィクトル・ユーゴー)
まだ読みかけだが、面白い本である。英語、中国語、日本語の読字において、脳の活性する場所が明らかに違う話とか、ソクラテスは自らはなにも書き残さなかったが、じっさいに彼が書字を嫌悪していたことなど、知らなかった話が多い。文字によって失ったものと得たものということから、『喪失と獲得-進化心理学から見た心と体』(ニコラス・ハンフリー著 垂水雄二訳)も再読したくなった。
文字が図形に見えたり、音節の区切りが狂って変なものに感じられることは、ときどきある。車を運転中、タンクローリーなどに書いてある「危」というマークに遭遇する機会は多い。あるとき、この漢字の「中身」は螺旋なんだと気づいた。そのときに頭に浮かんだのは、危険というのは台風に巻き込まれるようなものだ、しかし、向きが逆だ、南半球の低気圧か、といったことである。
次のようなこともあった。ある日、「ちょうふ」という駅名表記の「うふ」が気になってしかたがなくなったのだ。駅のホームのあっちでもこっちでも微笑んでいる。うふ。うふ。後日、この笑い声は甲府でも発生した。
疑似円筒凹多面体 ― 2008/10/25 11:28

「WONDA」は、多面体を構成する三角形が、合同の繰り返しではないのが特徴的だ。「FIRE」などのパターンを「ダイヤカット缶」と呼ぶのにたいして、「ブリリアントカット缶」と呼ぶらしい。
これらの多面体缶は、中身のメーカーはまちまちだが、缶はすべて東洋製罐という会社によるものである。そしてこれは、三浦公亮さんのPCCP(疑似円筒凹多面体)シェルという研究が基礎になっている。三浦先生は、以下のようなことをおっしゃっていた。
「工学的には強度を保ちつつ材料を減らせることに意味があるのだけれど、じっさいの製造では、機械の問題などもあって、板の厚さは変わっていないんだよね。デザインの面白さが主になっているんだ。意外な使われ方だね」
オイラーの多面体定理 ― 2008/10/28 01:12
で、変なことを思いついた。円柱をオイラーの多面体定理を満たすようにするには、どうすればよいかということである。ちなみに、オイラーの多面体定理というのは、単純多面体(閉じた多面体で、各面にも全体にもドーナツのような穴がない)に関して、頂点の数+面の数-辺の数=2となる、という定理である。
円筒(円柱)の缶は、円2つと切り開いた長方形ひとつからなる。ここで、柱面を平面に開くのがミソである。じっさいの多くのスチール缶でもそこには継ぎ目がある。これを「見えない辺」とする。すると、上と下の円も、ただの円ではなく、継ぎ目のところに頂点のある「一角形」になる。結果、頂点は2、面は3、辺は3(円周ふたつと継ぎ目)で、2+3-3=2になるではないか。
平面に展開できる面(可展面)であれば、曲面を含む立体も、平面にするために切り開いたところを辺に、その端を頂点にすれば、オイラーの多面体定理は成り立つ…のではないか。たとえば円錐は、錐面の継ぎ目を考慮すれば、頂点2、面2、辺2だ。うーん、ちょっとした発見をした気分だぞ。
これを思いついたのはついさっきだが、そういえば、最近『北園克衛詩集』で、妙な単語に出会っていた。
望遠鏡空間が怠けて楕円形になり、2角形になり、抛物線になり、溶けてしまつた。無色透明の美しい少年が水晶のパイプを喞へてカメラの中に現はれてくる。こんにちは、私の美しい白い写真師! 写真師はプラットフオオムの椅子にゐる。『硝子の夜の少年の散歩』(『円錐詩集』から)
2角形!
オイラーの多面体定理といえば、2年ぐらい前に読んだ『デカルトの暗号手稿』(アミール・D-アクゼル著 水谷淳訳)によると、この定理は、オイラーよりも100年前に、デカルトが見つけていたらしい。
また、オイラーさんに関しては、つい最近読み返した、森毅さんの『異説数学者列伝』の以下の文章が笑える。
数学のどの分野を渉猟してもオイラーの公式に遭うことは、関西の山野を散策して弘法大師の独鈷水に遭うようなものである。「関西の」とあるが、弘法大師は、ダウザーか井戸堀職人だったんじゃないかとしか思えないひとで、大師が見つけたという湧き水は関東にもたくさんあるように思う。
オイラーの多面体定理-つづき ― 2008/10/28 23:54
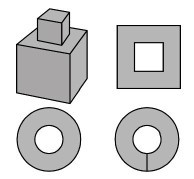
この例は、『数学小景』(高木貞治著)にあったものだ。立ち読みでしか見たことしかない本だったのだが、どこか記憶に残っていたのだろう、今日書店に寄る機会があって、確認した。
図右上のような穴の空いた面があることによって、辺(稜)のつながりが分断されてしまうことが、話のキモである。柱面(錐面も同様)も、グラフ(つながりを示す図)にすれば、左下のような穴の空いたかたちになる。これを切り開いて平面にすることは、右下のように、分離した要素であるふたつの同心円に連結させる道をつけることになる。「可展面を切り開いて平面にする」ことは、位相幾何的な問題ではないように思えるが、ここではグラフを繋げるということにもなっているわけだ。
なお、『数学小景』にも「二角形」、「もしも曲面で囲まれた多面体を許すならば」という記述があって、うなった。数学ファンなら読まなければいけない本だった。
また、もしかしたら、北園克衛氏の詩にある「2角形」もこの本がヒントかとも思ったが、『円錐詩集』(1933)は、『数学小景』(1943)より古かったので、これもうなった。











最近のコメント