ツイステッドコーン ― 2008/11/02 22:51

まず、その曲面の説明のために、写真上の曲面を説明しよう。これは、円に直径の折り目をつけ、その折り目を円の中心で折り返し、円錐をふたつ繋げたかたちにしたものである。
そして写真下である。これは、円に半径の切り込みをいれ、その分離したところを2回ひねって再接続した立体である。(追記:「2回ひねる」と書いたが、これは、後出のメビウスの輪のひねりを「1回」としてのことである。じっさいは「1回転ひねって」としたほうがわかりやすい)「再接続」するためには、面と面が交差することになるが、紙工作的には、接するところにちょっと糊をつけるというかたちできれいにまとまる。
ぐるりとひねったので、メビウスの輪と違って、面には裏と表の区別があることになる。よって、「メビウスの円錐」と呼びたいところをやめて、「ツイステッドコーン」とした。(追記:上記の追記と同じ理由で、最初つけていた名前から「ダブル」を取った)
この立体を「容器」として見ると、裏と表のどちらもが「内」にもなり「外」にもなっているのが面白い。
円からの立体は、「フォーチュンクッキーの幾何学」において、かなり考えたつもりだったのだが、あれは閉じたかたちにこだわっていた。そうでないものも視野にいれると、まだまだ「きれいなかたち」がありそうだ。
三枚重ね円錐、二枚重ね円錐 ― 2008/11/02 23:23
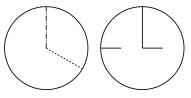
図右は、面が一様に二枚重ねになる円錐の展開図である。切り込みをいれることで糊を不要にしてみた。
『表裏同等折りの定義』再考 ― 2008/11/03 21:34

(1)ヘキサキューブの図:線の種別に誤りがあった。(上の図の赤い部分:上の図は修正済み)
(2)表中の人名でバルとあるのはハルが正しい。
自分の校正が甘いのに呆れた。ミスは恥ずかしいが、じつは、問題はそれではない。
自分の論文をひさしぶりに読んだのはほかでもない。この論文で提案した定義自体に疑問が生じたからである。
きっかけは、昨日の「ツイステッドコーン」 である。これは、直感的には、表裏同等と言ってよいモデルである。しかし、この論文の定義には反するのだ。
表裏同等というのは、川崎敏和さんの作例によって生まれた概念で、ざっと言えば「紙の表も裏も区別をつけられない折り紙モデル」のことである。たとえば、折り鶴は紙の外に出ているのは表で、紙の裏は完全に隠れる。(逆でもよいが同じことだ) しかし、折り鶴などと違って、表も裏も同じように現れるモデルがある。そうしたモデルの数学的特徴を見いだして、まとめたものが以下である。
表裏同等モデルとは、n回の回反対称 (n-fold rotational inverse symmetry) のモデルのことである。ただし、その場合の回転軸は展開された平面に対して垂直である。
(なお、「回反対称」(rotational inverse symmetry)というのは、「反転し、回転させると同じ図形になる」ということである。)
しかし、「ツイステッドコーン」はこれに該当しない。もっと単純な例を考えることもできる。例えば、図にあげたものだ。これも表裏同等折りに含めたほうがよいのではないか。これは、正方形の対角線を回転軸とした回転対称で、回反対称ではない。
豆に驚く鬼 ― 2008/11/04 21:49

食事の誘い ― 2008/11/08 12:08

これは水道パイプではない ― 2008/11/16 00:12

で、ここでは、会場の名古屋芸術大学にあった、謎の物件の話をしたい。
名古屋芸術大学・西キャンパスA404教室。教室後部のごく普通の壁に、いきなり蛇口がついているのだ。いかにも唐突で、洗面台や流しは影もかたちもない。写真に写っているのは、積み重ねた椅子である。
蛇口の周囲には、学生の手によるとおぼしき「特命リサーチ2001 こんなところに蛇口が!」「おどろくほどでます」「節水中」といったものや、でっちあげの因縁来歴など、この物件の非日常性に霊感を得た魂の叫び(?)がびっしりと書いてある。
てなわけで、芸術大学だけに、撤去するにできなくなった、とわたしはみた。単に掃除などで使うのかもしれないが…。いや、そんなことはない。あれは芸術である。インスタレーションアートなのである。「超芸術トマソン」である。
わたしとしては、この「作品」に、ルネ・マグリット画伯に敬意を表して「これは水道パイプではない」と名付けたいと思う。
なお、じっさいに水が出るのかは、コンベンション参加者の誰も、怖くて試していない。
ちなみに、「超芸術トマソン」という概念を生んだ名著・『超芸術トマソン』(赤瀬川原平著)の表紙写真は、銭湯の煙突の上に乗っての超広角レンズによる風景という忘れ難いものだが、これを撮った写真家・飯村昭彦さんが、ちょっとした縁で我が家に来たことがある。あとになって、あのアングルで写真を撮ってもらえばよかったと残念、なんてことも思い出している名古屋の夜なのであった。
[追記]:我慢できずに(?)、今日(11/16)じっさいに水が出ることを確認した。つまり、「これは水道パイプである」










最近のコメント