オイラーの多面体定理 ― 2008/10/28 01:12
で、変なことを思いついた。円柱をオイラーの多面体定理を満たすようにするには、どうすればよいかということである。ちなみに、オイラーの多面体定理というのは、単純多面体(閉じた多面体で、各面にも全体にもドーナツのような穴がない)に関して、頂点の数+面の数-辺の数=2となる、という定理である。
円筒(円柱)の缶は、円2つと切り開いた長方形ひとつからなる。ここで、柱面を平面に開くのがミソである。じっさいの多くのスチール缶でもそこには継ぎ目がある。これを「見えない辺」とする。すると、上と下の円も、ただの円ではなく、継ぎ目のところに頂点のある「一角形」になる。結果、頂点は2、面は3、辺は3(円周ふたつと継ぎ目)で、2+3-3=2になるではないか。
平面に展開できる面(可展面)であれば、曲面を含む立体も、平面にするために切り開いたところを辺に、その端を頂点にすれば、オイラーの多面体定理は成り立つ…のではないか。たとえば円錐は、錐面の継ぎ目を考慮すれば、頂点2、面2、辺2だ。うーん、ちょっとした発見をした気分だぞ。
これを思いついたのはついさっきだが、そういえば、最近『北園克衛詩集』で、妙な単語に出会っていた。
望遠鏡空間が怠けて楕円形になり、2角形になり、抛物線になり、溶けてしまつた。無色透明の美しい少年が水晶のパイプを喞へてカメラの中に現はれてくる。こんにちは、私の美しい白い写真師! 写真師はプラットフオオムの椅子にゐる。『硝子の夜の少年の散歩』(『円錐詩集』から)
2角形!
オイラーの多面体定理といえば、2年ぐらい前に読んだ『デカルトの暗号手稿』(アミール・D-アクゼル著 水谷淳訳)によると、この定理は、オイラーよりも100年前に、デカルトが見つけていたらしい。
また、オイラーさんに関しては、つい最近読み返した、森毅さんの『異説数学者列伝』の以下の文章が笑える。
数学のどの分野を渉猟してもオイラーの公式に遭うことは、関西の山野を散策して弘法大師の独鈷水に遭うようなものである。「関西の」とあるが、弘法大師は、ダウザーか井戸堀職人だったんじゃないかとしか思えないひとで、大師が見つけたという湧き水は関東にもたくさんあるように思う。
オイラーの多面体定理-つづき ― 2008/10/28 23:54
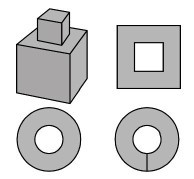
この例は、『数学小景』(高木貞治著)にあったものだ。立ち読みでしか見たことしかない本だったのだが、どこか記憶に残っていたのだろう、今日書店に寄る機会があって、確認した。
図右上のような穴の空いた面があることによって、辺(稜)のつながりが分断されてしまうことが、話のキモである。柱面(錐面も同様)も、グラフ(つながりを示す図)にすれば、左下のような穴の空いたかたちになる。これを切り開いて平面にすることは、右下のように、分離した要素であるふたつの同心円に連結させる道をつけることになる。「可展面を切り開いて平面にする」ことは、位相幾何的な問題ではないように思えるが、ここではグラフを繋げるということにもなっているわけだ。
なお、『数学小景』にも「二角形」、「もしも曲面で囲まれた多面体を許すならば」という記述があって、うなった。数学ファンなら読まなければいけない本だった。
また、もしかしたら、北園克衛氏の詩にある「2角形」もこの本がヒントかとも思ったが、『円錐詩集』(1933)は、『数学小景』(1943)より古かったので、これもうなった。











最近のコメント