ヴァリニョン畳紙(?) ― 2011/11/06 00:39

この定理の特殊な場合として、次のことがある。
・四辺形の2本の対角線が等しいとき、中点を結んでできる四辺形は菱形になる。
・対角線が直交しているとき、中点を結んでできる四辺形は長方形になる。
・上のふたつが満たされるとき、中点を結んでできる四辺形は正方形になる。
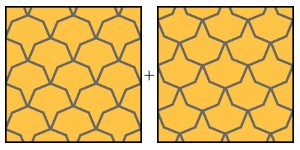
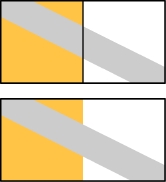
菱形になる四辺形には、長方形や等脚台形などがあるが、長方形でも等脚台形でもない、一見なんの特徴もなさそうな四辺形(上段中写真)がこうした条件を満たしていると、その四辺形には、隠れた特徴を持った「世を忍ぶ仮の姿」の風情がある。そして、正方形になる場合の隠れた特徴を確認する、じつに「折り紙的」な方法があることに気づいた。対角線の交点に合わせて「ざぶとん折り」をすると、正方形になるのだ(右上写真)。これがなかなかきれいなので、この特徴を使って、畳紙(パッケージ)をつくってみた。名づけて、「ヴァリニョン畳紙」(なんのこっちゃ)(中段写真:長方形用紙と正方形用紙)である。(←この段落、11/11 一部、正しくない表現を修正)
四辺形に内接する四辺形といえば、長方形に内接する菱形に関して、次のようなこともある。以前、菱形十二面体の折り紙モデルをつくっているときに気づいたことだ。
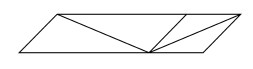
長方形に内接する菱形は、中点を連結したものが面積最小になり、長方形の頂点と菱形の頂点が一致するものが面積最大になるのだが、これらの菱形はすべて相似なのだ(図下段)。菱形の対角線の比が外の長方形の辺の比になることはすぐに示せるので、当たり前と言えば当たり前なのだが、これを見つけたときは、ちょっと意外の感があった。
なお、『偏愛的数学II 魅惑の図形』には、以前このブログに書いた「完全直方体」が不可能であることが証明されていた旨のことも書いてあった。
後記(2012/06/19) :座右の書でありながら、きちんと読んでいない『幾何学入門』(H.S.M.コクセター著 銀林浩訳)をぱらぱらとめくっていて、Varignonをカタカナ表記すれば、ヴァリグノンではなくヴァリニョンであるということに気がついたので、表記を修正した。
から四面体子 ― 2011/11/06 00:46

波の重ね合わせによる銀杏タイル ― 2011/11/10 00:02

向きの異なるふたつの同じ波線。それをすこしずつスライドして重ね合わせると、四方向の銀杏型のタイルができる。
同じ向き(図の正方形から22.5度傾いた方向)にスライドすることで四種ができるが、ループさせるためには、階段状の動きが必要になる。
銀杏タイルの重ね合わせ ― 2011/11/17 12:45

錯視の話 ― 2011/11/17 12:48

折鶴の絵 ― 2011/11/18 23:15

雰囲気があって、かつ、かなり正確に描かれたよい絵なのだが、つぎのような疑問がわきあがったのである。
疑問:折鶴の下にあるのは折り紙用紙だろうか。重なった折り紙用紙だとすると、折鶴にくらべて小さすぎるのではないか。
解釈を試みた。(以下、なぜか、AとBの対話形式である)
A:折鶴の下にある四角形は、四枚重ねのように見える。これは、二回折り畳んだ折り紙用紙ではないのか。右下の頂点がもとの正方形の4頂点が集まった点とみれば、写実的な絵である。
B:それでは話が終わってしまうではないか。たしかにそう見えなくもないが、四頂点がそろいすぎていないか。ふたつ折りの繰り返しとすれば、紙の復元力でもうすこし半開きになるはずだ。左側がやや開いて見えるので、二回目の折りを右から左の折りとして、厚みのある素材と考えれば、右側の二重線は、もとの正方形の縁ではなく、厚みを示す陰影のようなものと解釈できないか。素材に厚みがあるとすれば、紙から離れて、たとえば、これは、畳んだハンカチと見ることはできないか。
A:折り紙用紙の標準的な大きさは15cm四方である。折鶴がその用紙からつくられていると推測すると、この「ハンカチ」も15cm程度と見積もることができる。しかし、ハンカチの標準的な大きさは、男物で40数cm、女物の最小サイズ(ティッシュペーパーとほぼ同じサイズ)でも20cmである。サイズがあわないので、その解釈は難しいだろう。
B:折鶴も赤いハンカチで折ったと考えるのはどうか。折鶴が立体的に広げられていないが、これは、紙と布の剛性の違い、つまりやわらかくて立体的にすることができないからではないか。
A:布では、くちばしの部分をこのように正確に折ることは、きわめて難しいだろう。
B:それはたしかにそうだ。そもそも、折鶴をふつうに折る場合、ふたつ折りを繰り返すような工程を使うだろうか。できなくはないが、きわめて特殊だ。これは、一見、重なった正方形の紙や畳んだ紙やハンカチのように見えるが、折鶴の折りかたが示された豆本なのではないか。つまり、右側の線は、背表紙の厚みである。筑摩書房がそういう本を出すのかもしれない。
A:いくらなんでも考え過ぎだろう。
B:いや、考え過ぎというのは、次のようなことをいう。
このページの他の絵は、ベッドで本を読む女性、ペットボトルの影に隠れる猫である。ペットボトルは猫除けになるという説があるが、あれは眉唾で、水が温まっていれば猫が湯たんぽにすることもあるだろうし、冷えていれば、熱っぽい猫が体を冷やすこともあるだろう。さらに、このボトルの中身は水ではなく、凍っているとも考えられる。なぜなら、女(ジョ)⇔書(ショ)、猫(ビョウ)⇔氷(ヒョウ)という対応が成立するからである。すると、鶴(カク)に対応するのはガクである。すなわち、重なった紙のように見えるこの四角形は、小さな額のようなものなのである。
A:みごとに考え過ぎだ。図像学のパロディーのようだ。もっと、折り紙に即した説はないのか。
B:この折鶴は、ただの折鶴ではなく、小さな紙をモジュールとして組み合わせてつくる、画期的なユニット折鶴なのである。下にあるのはそのモジュールのための小さい紙である。筑摩書房が、ユニット折り紙の女王こと布施知子さんの本を出している出版社であることを忘れてはいけない。
A:君は暇なのか。これは単純に、対角線の折り目が省略された、折鶴の途中工程、いわゆる「正方基本形」だと思えばいいのではないか。
B:なるほど…。暇なのかという質問には、そうでもない、と答えるしかない。やるべきことから逃避しているけれどね。










最近のコメント