最大体積円錐とマラルディの角度 ― 2010/01/13 23:15

最大体積円錐
　今年になってから、ブログの更新が頻繁で、われながらどうしたのかと思うのだが、今日も更新である。どんなことにも「慣性」というものがあるのだろう。

さて。
　『本格折り紙』、『本格折り紙√2』と上梓したので、先日、次は何？と訊かれた。なんの考えもなく、反射で「√3とか」と応えると、同席していたひとが「πというのもあるよ」と言った。
　なるほどと思ったけれど、考えてみれば、すでに『折り紙π』に相応しい、三谷純さんの『ふしぎな球体・立体折り紙』という本がでたばかりであった。
　また、球面の折り紙の数学ついては、川崎敏和さんの研究が進んでいる。

　球面ではなく、円形膜の変形に関しては、まだ掘ることのできる鉱脈があるかな、とは思っている。『Origami4 - Fourth International Meeting of Origami Science, Mathematics, and Education』（R. J. Lang 編）に載った『フォーチュンクッキーの幾何学的系統樹』という論文は、わたしの中では、「円形折り紙」のいわば序説なのである。いつも、序説止まりなんだけれど。

　というように、円形膜の変形には、漠然とした関心を持っているわけだが、昨日、『機械じかけの数学-リーマンの定理、オイラーの公式への力学的アプローチ』（マーク・レヴィ著、松浦俊輔訳）という、買ったばかりの本をぱらぱらとめくっていて、その関心の釣り針にちょっとひっかかる、次のような折り紙的な問題に遭遇した。

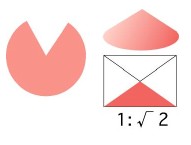
問題：円にひだ寄せて円錐をつくる場合、側面になる扇型の角度をどうすれば、最大体積の円錐になるか

　本では、この問題を変わった方法で解いている。最大体積の問題と、気体のはいった円錐の容器における側面と底面の力のモーメントが釣り合う問題が等しくなることを示し、それを解くのである。立体が単純だからこれで解けるとも言えるし、普通に解いたほうが早いとも言えるが、面白い。なお、そのとき、直接解く値は、展開された扇型の角度ではなく円錐の母線がつくる「頂角」である。

　いっぽう、普通に解く方法は、入試問題みたいな感じになる。式をたてて、微分してそれがゼロになる極値を求めればよい。扇型の角度で解けば、それは、(2√2/√3)πラジアン、度でいえば、293.938..度となる。なお、入試問題テクニック風に言えば、扇型の角度を変数とした関数で解くより、円錐の高さを変数として解いたほうがはるかに式が簡単になる。
　そして、この簡単さは、答えの「美しさ」にもつながる。扇型の角度は、いまひとつ「すっきりしない値」だが、円錐の母線がつくる「頂角」のほうは、おっと思う値になっているのだ。これは知らなかった。

　円錐の半径と高さの比が√2対1になる場合が、体積最大なのである。つまり、この円錐の母線のなす角度は、ダイヤモンドの結晶や蜂の巣の末端、石鹸膜などに見られる特別な角度「マラルディの角度」なのであった。

by maekawa [折り紙] [かたち・幾何学] [コメント(2)｜トラックバック(0)]