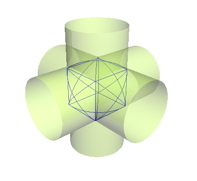
交差する円柱の共通部分 ― 2013/03/02 23:55




『宙の地図』 ― 2013/03/03 01:26
いまの望みはもう一度彼女に会うことだけだった。その目的に向かってつき進むのみ。だがそれだけでは足りない。彼女と知りあいになり、本当はどんな女性なのか、どんなお茶が好みなのか、子供時代の最も恐ろしい思い出はなにか、いちばんの望みはなにか、すべて調べるのだ。最終的には、折り鶴を開いてどうすればそういう形になるのかを解き明かすように、たたまれた彼女の心をきれいに広げてしまわなければならない。それが愛なのだろうか? 彼女が私の魂から欠け落ちたかけらなのか?
恋する男の独白的描写なので、書き写していてちょっと恥ずかしくなるというか、ストーカーだぞおい、と思うが、パルマ氏は、人生を折り紙に喩えるのが好きみたいである。
『時の地図』では、表記が「折りヅル」となぜかカタカナになっていて、スペイン語の原著では、「grúa del ppaer」(紙の鶴)などではなく「pajarita」(パハリータ:小鳥の意。スペインの伝承折り紙)だったのではないかとも思ったのだが、今回は「折り鶴」だった。
小説自体はたいへん面白かった。登場人物の多くが、端役にいたるまで、実在の人物であったり、他作家からの引用であったりする作風は、どこか山田風太郎さんに似ている。
「つるの小物入れ」 ― 2013/03/03 20:23

「これがそのときの折り鶴です」田村が浩二郎たちの前に置いた鶴は、確かに変わった形をしていた。
くちばしや尾、羽根の部分は普通の折り鶴なのだが、背中が四角く開いていて、そこが小物入れにになっていたのだ。
昭和四十年。集団就職で東北から上京した少年。彼は、工場の仲間と諍いをおこして街に飛び出す。路地裏のジャズ喫茶。少年はひとりの少女に親切にされ、おだやかに諭される。たった一回の短い出会い。それから40年余、折りにふれてその女性を思い出す男は、お礼を伝えたい、そのひとを探しだしてほしいと探偵事務所を訪ねる。手がかりは、すこし変わったかたちの折り鶴のみ。というような話である。
さて。この、背中が小物入れになっている折り鶴だが、これは、河合豊彰さんの「つるの小物入れ」であると見て間違いない。そして、この作品の初出は、保育社カラーブックスの『おりがみ』(復刻版あり)のはずである。ここで「問題」なのは、その出版年が1970年(昭和四十五年)ということだ。つまり、この折り鶴は、1965年には一般には知られていなかったはずなのである。
…と、野暮な「考証」をしてみた。
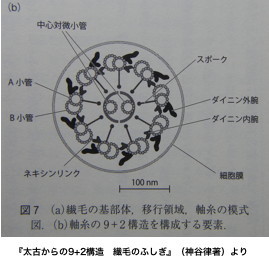
『太古からの9+2構造 繊毛のふしぎ』 ― 2013/03/05 22:25

山梨の読書生活など ― 2013/03/07 00:24

八ヶ岳山麓に向かう途中、珍しく甲府のジュンク堂に寄った。駅前にきれいな県立図書館がオープンし、岡島デパートのワンフロアがジュンク堂になって、甲府の読書環境はよくなった。ジュンク堂には、上のようなポスターが貼ってあり、おっと思った。
某月某日
京王線のダイヤ改正で「通勤快速」がなくなり、区間急行というものになっていた。
通勤快速と言えば、森村誠一さんの『通勤快速殺人事件』は、クリスティの『オリエント急行殺人事件』のパロディタイトルとして秀逸だった。大陸横断鉄道と満員の通勤電車。巷塵にまみれ、生活感がにじみ出た感じが、実にそれらしい。
読んでいないけれど、最近でた、青崎有吾さんの『体育館の殺人』も、綾辻行人さんの館シリーズがタイトルがネタだろうけれど、スケールの縮まった感じが逆によい味である。折原一さんの『脇本陣殺人事件』というのもあり、これは、わたしも思いついたことがあったので、「やられた」と思った。別に自分では書きもしないのに。
ミステリの本歌取りタイトルには、『Wの悲劇』(クイーン→夏樹静子)『弁護側の証人』(クリスティ→小泉喜美子)『なぜ絵版師に頼まなかったのか』(クリスティ→北森鴻)『鷲は飛び立った』(J.ヒギンズ→これは本人)などもある。
で、『線と面』というのはどうだろう。「線と面」というのは、折り紙のことでもあるが、アリバイを「高次元化」するとどうなるだろうかと。
ある時刻にある場所(点)にいることが証明されるのではなく、ある線上にいることだけが証明できるという設定である。たとえば、GPS衛星が壊れて、経度しか記録がないという状況。容疑者のいた場所も犯罪現場も経度がわかっている。それが離れているために不可能に思われた犯罪であったが、犯行は極付近で行われたので、経度が離れていても移動は簡単なのであった!…しょうもない話だな。
『数学セミナー』連載:『折って楽しむ折り紙セミナー』 ― 2013/03/09 17:20
『数学セミナー』は、かつて、伏見康治・満枝さんや戸村浩さんの連載があった雑誌で、なんというか、甲子園のマウンドにあがる気分です。
と、告知になると、なぜか「ですます調」になるのでした。











最近のコメント