交差する円柱の共通部分 ― 2013/03/02 23:55
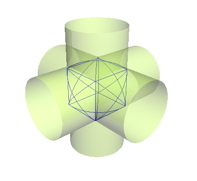
柱面が交差するモデルをいろいろ試して、三つの正四角柱、三つの円柱、三つの菱形四角柱（内部空間は正十二面体）のすっきりしたモデルができた。それぞれ同一ピース６枚組で
、無駄なく美しいのだが、前例がありそうな匂いがした。案の定、パズル関係者のひとたちに訊くと、浜野明千宏さんの「くみがみ」のハマノズキューブ他と、野町直史さんのノマチズアイコサヘドロン（追記3/12 これも、浜野さんが同じものを先に考案していることもわかった）と同じであることが判明した。残念といえば残念だが、発見の喜びはあった。
交差する円柱の共通部分の体積は、和算の資料でも見たことがあるが、大学入試問題の定番でもあるらしい。円柱の半径を1として、二円柱（左）なら、16/3、三円柱（右）なら16-8√2となる。πがでてこないのが面白い。
これを、積分を使わずに計算する方法を考えてみた。（ただし、球の体積、円錐の体積などは既知とする）
上は、ふたつの円柱の交差を半分に切ったモデルである。（ちなみに、切り込みは、サインカーブの一部になる）
見たとおり、二円柱の共通部分は、「カーブのついた四角錐状の立体」をふたつあわせたものだ。円弧に沿って大きさが変わる正方形を積み上げたようなかたちである。いっぽう、球は円を積み上げたようなかたちである。（「積み上げたかたち」というところに積分の発想がはいってしまっているけれど、それはそれ）
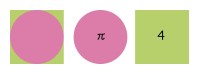
さて。正方形の面積とそれに内接する円の面積の比は4/πである。したがって、球と、ここで求める立体の体積の比も、円と正方形の面積の比と同じになる。半径1の球の体積は4π/3である。よって、求める体積は、4π/3×4/π=16/3と、単純なかけ算で計算できる。
三円柱の共通部分は、二円柱の交差と同じ「カーブのついた四角錐状の立体」の一部分(底辺が√2のところまで）が6つと、一辺√2の立方体があわさったかたちである。
この「カーブのついた四角錐状の立体」(底辺が√2)も、中心から√2/2の距離で切り取られた半径1の球の部分体積がわかれば、それに4/πを掛ければ計算できる。
ここで使えるのは、球をスライスした部分の体積の面白い特徴である。球をスライスした部分の体積は、球に外接する円柱を球のスライスと同じ面で切り取った部分円柱から、球の中心を頂点として円柱の円を底辺とする円錐面がつくる凹みを除いたトーラス状の部分（図左上）の体積に等しいのである。たしかアルキメデスによる発見で、ガリレオが『新科学対話』でも述べている。これは、
中心から距離xの平面で切断した時の球の断面積がπ(1-x^2)で、円柱から円錐台をのぞいた部分の断面（輪っか）の面積がπ-πx^2と、同じになるからである。
よって、錐体の体積=底面積×高さ/3 という公式を知っていれば、積分を使わなくても、次のように答えを求めることができる。
中心から√2/2のところで切り取った部分球の体積=円柱の体積-円錐台の体積=(1-√2/2)π-(π/3-( √2π/12))=(8-5√2)π/12
「カーブのついた四角錐状の立体」(底辺が√2）の体積=(8-5√2)π/12*4/π=(8-5√2)/3
三円柱の共通部分の体積=(8-5√2)/3*6+2√2=16-8√2
コメント
_ Joker ― 2013/03/04 00:08
_ maekawa ― 2013/03/05 22:23
「切り口の面積が常に等しい2つの立体の体積は等しい」ことを、カヴェリエリの原理ということは、初めて知りました。カヴェリエリはガリレオと同時代のひとですね。
日曜日に、図書館でガリレオの『新科学対話』の円柱・円錐・球の体積の話を確認してきました。ルカ・ヴァレリオの名前（現代のアルキメデスと称している）はありましたが、カヴァリエリの名はありませんでした。カヴァリエリの『連続体の不可分量による新しい方法の幾何学』が1635年なので、『新科学対話』(1638年）より前に出版されているのですけれどね。
なお、『新科学対話』は、昭和十一年の版をそのまま使っているという岩波文庫でした。
「みずすましの図工ノート」も見ました。
日曜日に、図書館でガリレオの『新科学対話』の円柱・円錐・球の体積の話を確認してきました。ルカ・ヴァレリオの名前（現代のアルキメデスと称している）はありましたが、カヴァリエリの名はありませんでした。カヴァリエリの『連続体の不可分量による新しい方法の幾何学』が1635年なので、『新科学対話』(1638年）より前に出版されているのですけれどね。
なお、『新科学対話』は、昭和十一年の版をそのまま使っているという岩波文庫でした。
「みずすましの図工ノート」も見ました。
_ maekawa ― 2013/03/20 16:19
↑岩波文庫『新科学対話』の版は昭和十二年でした。
コメントをどうぞ
※メールアドレスとURLの入力は必須ではありません。 入力されたメールアドレスは記事に反映されず、ブログの管理者のみが参照できます。
※投稿には管理者が設定した質問に答える必要があります。
トラックバック
このエントリのトラックバックURL: http://origami.asablo.jp/blog/2013/02/28/6733062/tb
※なお、送られたトラックバックはブログの管理者が確認するまで公開されません。
２円柱の共通部分は、3Dプリンタでプラスチックを積層させて作ったモデルを見たことがあります。まさに「正方形を積み上げたかたち」なのがよく分かりました。πが関係しないのが面白いです。
円筒と円錐と球と。伝説によれば、アルキメデスの墓のデザインがこれなのでしたっけ。「切り口の面積が常に等しい2つの立体の体積は等しい」というのは、カヴァリエリの原理ですね。
模様のブログ最近少し更新しました。こちらではみずすましと名乗っております。余計な話題ですが、お知らせまで。
http://j344.exblog.jp/