四次元的マラルディの角度 ― 2009/02/24 21:58
マラルディの角度というのは、度で言えば、約109.47度、正四面体の中心と頂点を結んだ線分のなす角度のことである。17-18世紀のマラルディという数学者が、ミツバチの巣や菱形十二面体などに現れる角度として示したものだ。わたしも、最近の立方体折り紙作品で使いまくっている。
細矢先生の話は以下のようなものだ。
二次元の図形・正三角形では、各辺の中心(各頂点でも同じ)から三角形の中心に集まる線分の角度は、120度になる。これは、cosθ=-1/2となるθである。三次元の図形・正四面体では、各面の中心(各頂点でも同じ)からの四面体の中心への線分がなす角度はマラルディの角度になる。cosθ=-1/3となるθである。そして、四次元の正五胞体(四次元空間で正四面体が5個合わさったかたち)では、それは、cosθ=-1/4になるというのである。5個の正四面体の中心を結んだ線のなす角度である。
なお、細矢先生の専門は化学だが、退官されてからは、以前にも増して数学に凝っているとのことだった。
この、cosθ=-1/4 (θは約104.48度になる)なる角度が、わたしが以前考えたまったく別の造形にあったのを、いまさっき、袋の口を留める針金入りのリボンをいじっていて、突然思い出したのである。
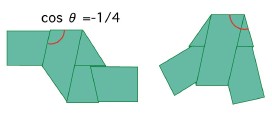
テープをふつうに結ぶと正五角形になることは有名である。しかし、それ以外のテープの結び目はあまり知られていないはずだ。変則的な六角形になる二種の結び(図)に現れる角度が、このcosθ=-1/4なのである。この結びかたは単に「六角結び」と名付けていたが、「四次元のマラルディの角度による六角結び」というのも、仰々しくてよいかもしれない。
テープ曲面 ― 2009/02/24 22:03












最近のコメント