エッシャー風折鶴ステンドグラスとピックの公式 ― 2012/07/23 23:37
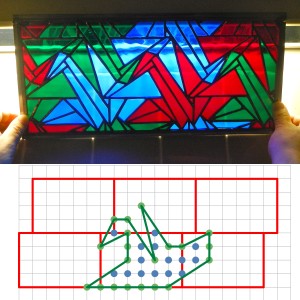
「エッシャー風折鶴」(デザイン:前川淳 製作:前川純子(すみこ))
デザイン自体はかなり以前のもので、基本は、図のように、4×6の長方形を、格子点を基準に、出っ張らせたりへっこませたりしてつくったものである。
格子点を結んだ多角形と言えば、昨日の書き込み・「円周率近似値の日」にもそういった図形がでてきたが、こうした図形に当てはまる「ピックの公式」というものがあって、これが面白いので、紹介しておこう。意外性があって、実用性もあるのだが、それほどは知られていない式である。
ピックの公式
頂点が等間隔の格子点にのる、穴のない多角形の面積は、つぎのように求められる。
内部に含まれる格子点の数をP、辺にのる格子点の数をQとすると、面積Sは、S=P+Q/2-1である。
この式の発見者・ゲオルグ・アレクサンダー・ピックは、ユダヤ系のオーストリア人数学者で、アインシュタインと親交があったというひとだ。長生きはしたが、1942年7月26日に強制収容所で亡くなっている。明々後日が70年目の命日になる。
折鶴のかたちの面積をピックの公式で計算すると、内部に含まれる格子点が15、辺にのる格子点が20で、15+20/2-1=24と、もとの4×6の長方形と同じであることが確認できる。(なお、ピックの公式は、しきつめられる多角形のみのものではないので、そこは誤解なきよう)










最近のコメント