π> 3.05 ― 2012/07/19 21:19
この計算は、三角関数の公式を使わなくてもできる。折り紙好きならおなじみの三角形、22.5度の鋭角を持つ直角三角形は、短辺を1とすると、長辺は1+√2になり、斜辺は√(4+2√2)になる。ここで使うのは、二等辺三角形の性質やピタゴラスの定理だけだ。正八角形はこの三角形を16個集めたかたちである。つまり、これは中学生でも解ける問題である。
ただ、ここから導かれる8/√(4+2√2)>3.05という不等式が正しいことを示すための手計算は、それなりの手間がかかる。√2<1.42といった近似値を使うと、すこし楽になるが、この近似値をきちんと示すことも必要だ。
もっとエレガントな解答はないかと、考えてみた。
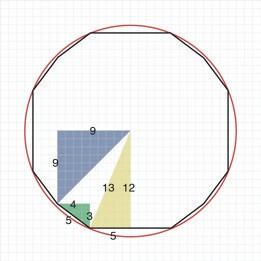
整数のみの計算にするために、5:12:13と3:4:5の直角三角形を使ってみた。すると、半径13の円と、8つの点が円に接して4つの点が円の内側にある、図のような変則的な十二角形がよい案配になった。(8点が円に接するのは、黄色い直角三角形の斜辺が13になるので明らかで、4点が円の内側にあり、外に凸なのは、12*12<9*9*2<13*13なので明らかである)
この十二角形の周囲の長さは80になる。 手計算は簡単で、
π>40/13=3.07..>3.05となる。
コメント
トラックバック
このエントリのトラックバックURL: http://origami.asablo.jp/blog/2012/07/19/6516445/tb
※なお、送られたトラックバックはブログの管理者が確認するまで公開されません。










コメントをどうぞ
※メールアドレスとURLの入力は必須ではありません。 入力されたメールアドレスは記事に反映されず、ブログの管理者のみが参照できます。
※投稿には管理者が設定した質問に答える必要があります。