立方体の二分割など ― 2018/05/25 22:36
明日、5/26（土）22:45-23:00に、NHK-Eテレで第12話が放映される。
明日から、折紙探偵団九州コンベンション（＠佐賀大学）に参加する。三枚組みの正八面体を講習予定である。
◆武蔵野美術大学の案内チラシ
武蔵野美術大学のオープン・キャンパス（6/9,10）の案内が、なんとなく折り紙的だった。こうした切れ目と折り目の「動き」に注目することは珍しくないが、置く（一見アンバランスに見える状態に）という機能に注目したのははじめて見た。
なお、同大学では、先週、非常勤講師をつとめた。講義では、立体感覚の面白さ難しさを味わうモデルとして、「穴のある包み紙（type 2）」のワークショップなどをおこなった。下の図がその用紙形である。表裏同等構造によって、きれいに閉じた立方体になる。
◆立方体の二分割、正四面体の二分割
「穴のある包み紙」に関連して、双曲放物面（図右上）を近似する折り目を、同心正方形蛇腹以外で実現することを考えていて、面白いかたちを見つけた。
右・中の図のような折り目をつけて、面角を変えてみる。すべての折り目は連動し、合同の二等辺三角形４面の四面体に内接するように連続的に変形する。ただし、それは、剛体構造ではない。中央の正方形がたわむのである。しかし、それは常にたわんでいるのではなく、平坦になるときもある。外接四面体が正四面体で、かつ中央の正方形が平坦になる折り目のとき、どのような折り目の角度になるか。それは、図に示した直角の1/4を基準とする折り目で近似できる（ぴったりではない）、ということが今回気がついたことである。
この目安は折りやすいので、さっそくこれを用紙の中心に埋め込んだモデルをつくってみた。全体を表裏同等モデルにしても面白いのだが、この折り目が内部に隠れてしまうので、二分割の立体にしたところ、造形的にも面白いものになった。
この折り目は、同じ折り目をさらに中央の正方形に当てはめて、入れ子構造にすることができる。するとそれは、変形で面が歪まない折り目になる。ただし、これは新発見ではない。同心正方形の折り目に対角線を加えるという「舘-ドメインモデル」と同様である。
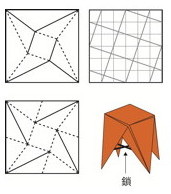
なお、正方形の折り目の辺は、用紙の辺と平行である必要はない。次の図（左上）はその例だ。これは、中心の正方形が平坦なとき、ねじり折りした三角形の面どうしが同一面になるように決めたものだ。
この折り目をすこし折り変えると、きれいな椅子のかたちになる。それは剛体折りなので、ヒンジと板でできる「折り畳み椅子」になる。ただし、平坦になるほうに力が働くことがあるので、これに対するためには、脚部を鎖でつなぐといった方法を適用しなければならない。それを外すと畳めるわけである。まあでも、踏み台に使うにはやや怖い構造だ。
◆三角柱箱
先日の正四面体の箱の姉妹モデルとして、正方形用紙から正三角柱の箱を考えた。チーズっぽくてよい。三角形の1辺を1とすると、高さは√3/3なので、体積はぴったり1/4である。きっちり閉じる構造にしたため、開けるのはすこし難しくなった。
コメント
トラックバック
このエントリのトラックバックURL: http://origami.asablo.jp/blog/2018/05/25/8859691/tb
※なお、送られたトラックバックはブログの管理者が確認するまで公開されません。
コメントをどうぞ
※メールアドレスとURLの入力は必須ではありません。 入力されたメールアドレスは記事に反映されず、ブログの管理者のみが参照できます。
※投稿には管理者が設定した質問に答える必要があります。