三十二面体など ― 2012/07/03 22:34

デイケアセンターが会場で、そこに、写真のようなものがあった。注目したのは、「ボール」が三十二面体(切頂二十面体)だったことだ。「シャッフル&ゴルフ」というものらしい。
この「ボール」にちょっと似たもので、プールの底に沈めて潜水訓練の目印に使うゴムの正二十面体を持っている。名前はなんというのだろうかと、ウェブで検索すると、マルチサイドダイブボールなるものがでてきた。これは、正二十面体ではなく、フラーのいう、2 frequency icosahedronである。
##
3連戦3連敗に5点差逆転負け、果ては、9回2アウトから2ラン逆転振り逃げ負けと、阪神タイガースの負けかたが、懐かしいダメっぷりになっている。
17 ― 2012/07/08 09:44
ウィークボソンやグルーオンには種別があるし、重力子は標準モデルには直接かかわってこないはずで、重力まで統一的に説明するためにはさらに粒子が必要になるだろうから、17種という言い方は適切とはいえないんじゃないの、と思ったわけなのであった。
なぜ17という数に反応したかというと、2次元のタイリングパターンが17種であることを連想したからで、素粒子の対称性とこれに関係があるの?と一瞬思ったからであった。
##
17と言えば、先日、和算の問題を解いていたときにでてきた答えが102だった。17×6である。これは5, 12, 13というピタゴラス数(a^2+b^2=c^2)の5と12から得られる値だった。「きれいな答え」をださせる問題に感心した。
年齢との連想だと思うけれど、11,13,17,19といった「ティーンエイジ」の素数は、なんか爽やかな感じがして、でてくると、「?!」と思うってひとは、けっこういるんじゃないかなあと思う。17年ゼミとか俳句十七音、十七条の憲法が「爽やか」かっていうと、なんとも言えないけれど…。
(後記:そういえば、定規とコンパスによるガウスの正17角形の作図というのもあったな)
なお、素粒子の数は、『銀河ヒッチハイクガイド』的には42種であることを期待したい。
(7/12:ヒッグス粒子をゲージ粒子に含めていたような記述を修正)
円周率の999999と7777 ― 2012/07/13 20:47

まず、111、555、000ときて、次が、小数点762桁からの999999なのだ。9の6つ並びである。100万分の1の確率で現れるであろうものが800桁ぐらいにででてくるのだ。
なお、円周率の計算が700桁以上なされたのは第二次世界大戦後になってからなので、この9の並びを見ることができたのは、けっこう最近のことになる。最初にこれを見たひとであろう、1947年に808桁まで計算したD.F.ファーガソンは、たぶん自分の計算間違いを疑っただろう。
1588桁までには、この999999の他に、000(2回)、111(2回)、555(3回)の3つしかでてこず、222、333、444、666、777、888はない。
19世紀に、論理学のド・モルガンの法則で有名なオーガスタス・ド・モルガンが、600桁までを見て「7が少ない」ということを指摘しているという。こうした偏りは、さらに桁を増やすと減って行くのだが、500億桁以上計算したのちにも偏りはあり、ほんのわずかながら最も多いのは5だという。なお、ド・モルガンが参照したのは、同時期にウィリアムス・シャンクスが計算して発表した707桁までのものと思われるが、これは、1945年、ファーガソンによって、527桁以降の誤りが発見されることになったものである。
(参考:『πの神秘』(デビッド ブラットナー著 浅尾敦則 訳))
というわけで、7が少ないようにも思えたのであるが、次にでてくる「ぞろ目」は、1589桁からの7777という7の4つ並びなのであった。ちなみに、1589は227×7と7で割りきれる。さらにこの227は、49番目の素数と、妙に7に関係する。
以上、「数秘術的」なものというか、数学的な論理性はない(だろう)けれど、面白い。
##
AppleのMobileMeの終了で、知り合いの鳥海太郎さんのページが引っ越した。URL転送サービスもないようなので、検索にかかりやすくするための一助として、ここに新アドレスを書いておく。 鳥海太郎の版画 TARO TORIUMI (http://www.yasakanet.ne.jp/~ttaro)
うねる陳列棚 ― 2012/07/16 15:50

π> 3.05 ― 2012/07/19 21:19
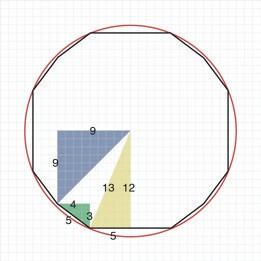
この計算は、三角関数の公式を使わなくてもできる。折り紙好きならおなじみの三角形、22.5度の鋭角を持つ直角三角形は、短辺を1とすると、長辺は1+√2になり、斜辺は√(4+2√2)になる。ここで使うのは、二等辺三角形の性質やピタゴラスの定理だけだ。正八角形はこの三角形を16個集めたかたちである。つまり、これは中学生でも解ける問題である。
ただ、ここから導かれる8/√(4+2√2)>3.05という不等式が正しいことを示すための手計算は、それなりの手間がかかる。√2<1.42といった近似値を使うと、すこし楽になるが、この近似値をきちんと示すことも必要だ。
もっとエレガントな解答はないかと、考えてみた。
整数のみの計算にするために、5:12:13と3:4:5の直角三角形を使ってみた。すると、半径13の円と、8つの点が円に接して4つの点が円の内側にある、図のような変則的な十二角形がよい案配になった。(8点が円に接するのは、黄色い直角三角形の斜辺が13になるので明らかで、4点が円の内側にあり、外に凸なのは、12*12<9*9*2<13*13なので明らかである)
この十二角形の周囲の長さは80になる。 手計算は簡単で、
π>40/13=3.07..>3.05となる。
円周率近似値の日 ― 2012/07/22 00:39

○図左上:直径28の円になるべく沿わせて、頂点が格子点上に乗るように、周囲の長さが88になる十二角形(みどりの線)を描いた。88/28=22/7なので、π≒22/7を表す図になっている。ただ、一部、円がかなりはみ出している。そこで、同じ格子で、はみ出した部分も円弧に近づけて十六角形にしてみた。(図右上)
○図右上:この十六角形の面積は、頂点が格子点にあるので容易に計算でき、616になる。高さと幅は28である。円の面積πr^2から、π≒616/(14*14)となるが、616は、なんと、14でうまいことに割り切れて44になる。すなわち、この図は、面積によってπ≒22/7を表す図になっている。これはきれいだ。
○図左下:さらに、円周率の近似値として知られる、π≒√10=3.162...を表す図を描いてみた。みどりの線が周囲の長さ8√5の八角形で(1:2の長方形の対角線の長さは√5だ)、赤の線が直径4√2の円である。8√5/4√2=√10なので、π≒√10を表す図になっているというわけである。これもなかなかきれいな図だ。
○図右下:π≒√2+√3=3.146...を表す図も描いてみた。1:√2の長方形を、図のように敷いて、それを使って八角形を描く。その周囲の長さは4(√2+√3)になる。赤い線は、長方形の短辺を定規にして描いた、直径4の円である。










最近のコメント