7OSMEなど ― 2018/09/02 22:31
◆浅野真一個展 わたくしといふ現象
サロンモザイク（大阪市北区天神橋1-14-11 天神ビル1F）にて、9/1(土）〜9/17（月）、具象画家・浅野真一さんの個展が開催中だ。折り紙をモチーフにした絵もあるという。（わたし自身は、残念ながら見に行けない）
◆7OSME
7OSME（第7回折り紙の科学・数学・教育国際会議）とBOS（イギリス折り紙協会）コンベンションに参加するため、明日から渡英。台風21号から逃げるみたいなかたちである。
7OSME（第7回折り紙の科学・数学・教育国際会議）とBOS（イギリス折り紙協会）コンベンションに参加するため、明日から渡英。台風21号から逃げるみたいなかたちである。
◆空-地球錯視
以前、空を撮った写真を180度回転させると、宇宙空間から撮った地球の写真のようになるという話を見た。この写真は、それを試してみたものだ。上がそのままで、下が180度回転させたものだ。たしかにそうなっているように見えなくもない。
これは、「クレーター錯視」の一種だと思われる。クレーターの写真を180度回転させると、凹みが山に見えるという錯視だ。クレーターの場合、その錯視の要因は主に陰影によるものだが、空の写真の場合はそれとは異なる。その理屈をすこし考えてみた。
空は、視点を中心にした球面の一部分として目に映る。目だけではなく、標準レンズでもそのように映り、広角レンズならなおさらである。まずは、雲の連なりなどから、球面座標を自然に読み取るのだろうと考えられる。それを上下逆にすると凸に見えるということだが、ここが簡単ではない。
球面を「自然」に読み取るとして、その座標だけを描くと、図のようになる。
180度回転させた図の下は、下側への半球を中からみた図であると認識しても不思議ではない。ただ、ここで注意すべきなのは、そのような画像を見る機会はないということだ。空は上にあって、巨大な凹面を見下ろすということは、まずない。いっぽう、現代人は、宇宙空間から見下ろした地球の画像というものを見慣れている。上下反転させた空の画像は、それにあてはめて、中心が凸になったように見えるのではないか。
つまり、これが凸に見えるのは、類似の画像を見慣れたことにもよる、とも考えられる。となると、以前、このブログに以前書いたポオの『軽気球夢譚』にあった、高空からは地表が凹面に見えるという現象も、じっさいにある（あった）ような気もしてくる。
下の写真は、野辺山宇宙電波観測所にある日本初の電波望遠鏡（1949）のレプリカをいれて空を撮ったものである。上下反転させると、人工衛星からの画像のように見えなくもない。
7OSME ― 2018/09/07 06:02
日本を離れてから、関西や北海道がたいへんなことになっている。
心配しながらも、この季節は気候穏やかにして、学問の街の代名詞的なオクスフォードでの7OSME（第7回折り紙の科学・数学・教育国際会議） に参加中である。
今回は、論文集が４分冊もあって、毎回、会が大きくなっていくのを感じる。
全体会では、時枝正さんによる、メビウスの輪の話を文字通り「すこしひねった」講演など。その全体会の会場は、その名も「Andrew Wiles Building（アンドリュー・ワイルズ棟）であった。建物の正面玄関前がペンローズタイルになっていて、玄関入ってすぐの敷石には、ギリシア語で「AΓEΩMETPHTOΣ MH∆EIΣ EIΣITΩ」（ 幾何学を知らざる者は、この門をくぐるべからず）が刻まれていたり、カフェの名前が「π」だったり、なかなか「遊んで」いるのであった。
下の写真は、「遠足」でいった、オクスフォード大学Harwellキャンパス、Oxfort Space Systemsの展開アンテナのデモンストレーション。
わたしの今回の発表は、"Connected Paper Cranes by using Continued Fractions and Progressions"（連分数と数列を用いた連鶴）というもの。
上の写真は、その一例の、πを正則連分数で表した連鶴である。なお、π/4をちょっと特殊な連分数で表す「ブラウンカーの式」に基づく正方形タイリングができていないとしたのだが、発表後、聴いていた村上友哉さんの示唆があって、簡単にできた。なんで気がつかなっかたのか... まあ、そういうこともあるよね。ただ、じっさいに折るのは難しそう。
7OSME（つづき） ― 2018/09/08 15:29
来るときに、飛行機の窓から見たブリテン島の南東にあった、洋上風力発電所。奇妙な風景だった。
7OSME終了。
今日からBOS（イギリス折り紙協会）のコンベンションに参加。
今日からBOS（イギリス折り紙協会）のコンベンションに参加。
写真を撮るのは川村みゆきさんにまかせた（？）のだけれど、いくつか。
右端に写っているのが発表会場のホールの裏側。個人の家みたいな建物も事務などに使われているみたいだ。「大学」の雰囲気が違う。
ドミトリー（個室だからゲストハウスというのかな）の窓からの眺め。わたしの棟は、トイレとシャワー共同だったけれど、窓から見る中庭に雰囲気があって、いまさっきもリスが樹をのぼっていた。
最終日の全体公演の舘知宏さんは、才気が全身からあふれるように颯爽としていた。折り紙は既にユニバーサルだし、日本がどうのはないのだけれど、舘さんと三谷さんという若く優秀な研究者が近くにいるというのは、たいへんありがたい。
今回概要を知った研究もいくつか。思いついたものをふたつ。
チェアを務めた「剛体折り紙その1」セッション（といっても、この発表は曲線折りを扱ったものだけれど）での、最小作用によって「自然な」曲面を決めるジェイコブ・バジャーさんらの研究。曲線折りは、折り目だけを決めても、拘束条件がないと自由度が高く、母線の選びかたも任意性が高い。それをエネルギーがミニマムになるように決める。錐面になりそうなものが、接線曲面になるというのは、直感にも合っていて、結果がきれいだった。
作図セッションでの、アダム・ウォーターハウスさんによる、折り紙作図を、誤差の観点で見る話。折り紙コミュニティーに直接関係する萌芽的な研究として面白かった。誤差の蓄積はどうなるのかなど難しい問題が多いけれど、そもそも、折り紙を折るときに、点を合わせるのがよいのか、線を合わせるのがよいのか、じっさいの紙では厚みをどう逃すかなど、折紙者ならみな経験的に持っているノウハウは、案外言語化されていない。厚みを逃す話では、厚みのある剛体折りの話題もいくつかあったし、初日の講演セルジオ・ペレグリーノさんの大面積構造物の折りたたみのために、折り目にスリットをいれてしまう方法（KIRIGAMIと呼ばれている）も関連している。
工学系、応用系の発表は、セッションがパラレルになっていて、ほとんど聴き損ねた。
サイエンスとアートを結びつける仕事をしているマシュー・ガーディナーさんなど、旧知のひとにも会って（何人かは、顔と名前が結びつかなくて失礼なのであった）、充実した会だった。
7OSMEと42 ― 2018/09/11 23:45
◆42
今日夕方、イギリスから帰宅した。
今日夕方、イギリスから帰宅した。
帰国便のヒースロー空港で、ゲート番号が42であった。そして、往きのシート番号が42だった。42は、日本では縁起の悪い数字だが、ブリティッシュ・ジョーク的には、最高の数字だ。
7OSMEでも関連した話があった。幾何作図セッション、ホルヘ・ルセロさんの「３次元ユークリッド空間の折り畳み」という話で、３次元空間を「折り面」で「折る」操作が50種になるという内容があり、そのさい、（聴き間違いでなければ）「42でないのが惜しい」というコメントがあったのだ。「あのネタ」として間違いないが、ちょっとわかりにくい。誰もがぽかんとしている感じだった。これは、おふざけSFの傑作『銀河ヒッチハイク・ガイド』（ダグラス・アダムス）にある、「生命、宇宙、そして万物にたいする究極の疑問の回答」が「42」であるというネタであろう。イギリスだし。
わたしのイギリス旅行も、銀河ヒッチハイクガイドに祝福されていたのであった。最近翻訳の出たアダムスさんの『長く暗い魂のティータイム』（安原和見訳）では、ヒースロー空港が爆破されていたけれどね。
◆ブラックウェル書店、そして『文字渦』
日曜日、7OSMEとBOSコンベンションのすべての日程が終わったあと、オクスフォード市内を散歩し、書店を何軒かはしごした。古書も扱っている店には、留学生か研究者の置き土産なのか、日本語の本もあって、興味深いものがあったが、中でも、世界的に有名な書店・ブラックウェルのたたずまいは雰囲気満点だった。地上の入り口からは想像のつかない広大な地下の空間に、本が満ちている。日曜日は17:00に閉まってしまったので、帰国日の朝もスーツケースをひきながら寄って、小一時間過ごし、使う本、読む本というより、『オクスフォード数学辞典』と、ワイルの『シンメトリー』とアボットの『フラット・ワールド』のペーパーバックを、お土産に買ってしまった。で、『オクスフォード数学辞典』と『Origami ^7』で記念写真。
日曜日、7OSMEとBOSコンベンションのすべての日程が終わったあと、オクスフォード市内を散歩し、書店を何軒かはしごした。古書も扱っている店には、留学生か研究者の置き土産なのか、日本語の本もあって、興味深いものがあったが、中でも、世界的に有名な書店・ブラックウェルのたたずまいは雰囲気満点だった。地上の入り口からは想像のつかない広大な地下の空間に、本が満ちている。日曜日は17:00に閉まってしまったので、帰国日の朝もスーツケースをひきながら寄って、小一時間過ごし、使う本、読む本というより、『オクスフォード数学辞典』と、ワイルの『シンメトリー』とアボットの『フラット・ワールド』のペーパーバックを、お土産に買ってしまった。で、『オクスフォード数学辞典』と『Origami ^7』で記念写真。
いまどき紙の本なんてと思うひとも多いと思うが、旅行の飛行機や列車で紙の本を読むのを楽しみにしていて、やっぱりなぜか紙の本がよいというひとも多いのではないか。今回のわたしも、荷物になるのに、とか言われながら、日本からも、会に関係ない本を3冊持っていって読んだ。
帰りの飛行機の中で読んだのが、円城塔さんの『文字渦』である。全編、手のこんだ冗談のような話のひねくれ具合がよくて、紙の本ならではの読書のたのしみにもあふれていた。さまざまな「情報」が詰め込まれているので、それをあれこれ考えるのもたのしそうだ。なお、次の箇所はちょっと気になった。
いわゆるプラトン立体である。ここで、六面体の角を綺麗に落としてやると八面体に、十二面体の角を綺麗に落としてやると二十面体となり、逆も成り立ったりして興味深い。（略）ちなみに、四面体の角を綺麗に落とすとまた四面体が現れて、自分自身で循環している。
正多面体の双対関係を述べており、間違いではない。しかし、プラトン立体をおぼろ気にしか知らないようなひとに説明する直感的な表現としてはややわかりにくい。正多面体の双対関係を直感的に示すなら、「角を落とす」より、「面の中心を結ぶ」にしたほうがよい。
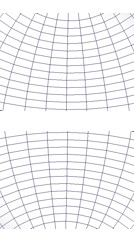
たとえば、「六面体の角を綺麗に落とす」と言ったとき、多くのひとは、図下・左のような切断面（円で表示）を思い描くはずである。小説を読んでいて、幾何図形を確認するひとは少ないだろうけれど、思い描いたとすれば、このような図ではないだろうか。
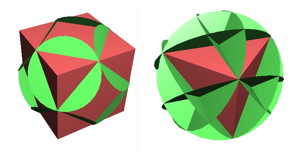
しかし、この図でできるのは、正八面体ではなく、立方八面体、つまり、立方体と正八面体をミックスしたようなかたちである。正二十面体、正十二面体でも同じで、「綺麗に角を落とす」と、立方八面体と同様、準正多面体の二十・十二面体になる。正四面体も同様で、辺の中点までで切り落とすと、正八面体になる。
「間違いでない」というのは、図下・右のように、切り落とす面を中心に近づけて交差するようにして切れば、面の中心を結ぶのと同じことになるからだ。しかし、この図を想像するのは、かなりのマニアである（なんのマニアだ）。
折り紙教室 ― 2018/09/13 21:26
◆折り紙教室＠第8回ダリアの華展
◆折り紙教室＠府中
9/24（月・祝）13:00-15:00、作品：うさぎ（写真）
9/24（月・祝）13:00-15:00、作品：うさぎ（写真）
10/8（月・祝）13:00-15:00、作品：ハロウィンのカボチャ
9月24日は太陰太陽暦で八月十五日、中秋の名月なので、うさぎである。うさぎは何種類か創作していて、これは、尻尾と耳の長さに特徴のあるタイプで、15年ぐらい前に小松英夫さんの図でイギリス折り紙協会の図集に掲載したものだ。
月と兎ということでは、最近知った次の古い俳句がよい。
兎ならちと出て遊べ月の中 八町
『新編 俳諧博物誌』（柴田宵曲著、小出昌洋編）より
「月の中」というのは、月光の中ということで、あんたの親玉は玉兎とかなんとか言って月にゆかりがあるのだから、このきれいな月夜、姿を見せて愛嬌をふりまけ、みたいな句である。宵曲によるこの句の解説はさらりとしたものだが、月と兎という定番の組み合わせをすこしだけ俳味でひねったところがわかりやすく、岩波文庫『俳諧博物誌』の表紙の内容紹介にも採られている。もっと広く知られてよい句だとも思うのだが、作者の八町というひとはどういうひとなのか、ざっと調べた限りでは、まったくわからず、そのことからも、俳諧の裾野の広さと、宵曲の、万巻の書を読む博識がわかる。宵曲の『古句を観る』の「はじめに」には、次の言葉もある。
世に持囃（もてはや）される者、広く人に知られたものばかりが、見るべき内容を有するのではない。各方面における看過されたる者、忘れられたる者の中から、真に価値あるものを発見することは、多くの人々によって常に企てられなければならぬ仕事の一であろうと思われる。
専門家と愛好家がフラットに並びうる分野のひとつである折り紙においても、示唆的な言葉だ。
なお写真の皿は、月面と宇宙飛行士をかたどった蚊取り線香立ての灰受け皿。
世界を変えた書物展 ― 2018/09/17 22:54
昨日、予定されてた会合がキャンセルとなったので、急遽予定を変えて、時間があれば行きたいと思っていた展覧会に行った。上野の森の美術館で開催中(-9/24）の「世界を変えた書物展」、金沢工業大学所蔵の科学（主に物理、数学）の貴重図書の展示である。驚くべきラインナップで、ニュートンの『プリンキピア』、デカルトの『方法序説』、ガリレオの『星界の報告』などのいずれも初版。オイラーやライプニッツ、ボヤイやリーマンなどもある。この展覧会、なんと無料で写真も自由。ということもあってか、とても混んでいたが、行っておいてよかった。
ミュージアムグッズにも面白いものが多くて、ケプラーの『世界の調和』から採った多面体の図を配した傘を買った。写真は、その傘と、傘ごしに見た我が家の多面体。
最近のコメント