『千代紙 折紙』 ― 2011/02/06 22:22
このシリーズで、既に持っていたものは、『紙』『数』『石』『野球』であった。『石』は最近買ったものだ。われながら、たいへんわかりやすいラインナップだと、笑ってしまった。
昨日、本巻の『宙』『藝』、別巻『星座』を入手した。『藝』をもとめたのは、ウェブのリストを見ていて、『千代紙 折紙』(芝木好子著)という一編があることを知ったためである。芝木さんが河合豊彰さんを訪ねた話が記されていた。
なにごとにせよ、初めに創り出すことが大変であり、意義があるのは言うまでもない。模倣は少しも苦労ではない。河合氏は今の具象から次第に抽象へゆきたいと考えているそうである。しかし、どの道一枚の四角い色紙のなかからあらゆる可能性を引出して、一つの造形のゆきつくのだから、新しく生まれたものを手にする時の思いは格別だろう。(『千代紙 折紙』芝木好子著 『杏の花」1977より)
四角の中の五角 ― 2011/02/07 21:47

四角錐は、側面が正三角形のもの(つまり正八面体を半分にしたもの)である。
底面と切断面の二面角は、tanθ=1/φ(φは黄金比)となるθ(約31.7度)である。
四角錐が「素直な」比率だったのは、ちょっと予想外だった。
四角の中の五角 その2 ― 2011/02/09 21:30

『四角の中の五角』といえば、アメリカ国防総省ペンタゴンがそうなっている。正方形の区画の中にペンタゴン(五角形)があるのだ。ただし、当初はきれいな正方形だったワシントンD.C.であるが、いまは、ポトマック川の西側はワシントンD.C.ではない。国防総省もそこにある。
四角の中の五角 その3 ― 2011/02/12 23:13

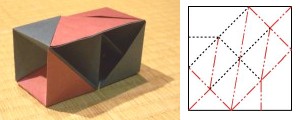
さらに、より「折り紙的」技法ということで、透明素材による一枚折りを試してみたものが、図・写真下である。まとまりのよさを優先して、展開図の対称性はくずした。
「合格→五角」ということで、合格のお守りにどう?
ふたつの立方体 ― 2011/02/13 09:32
四角の中の五角 その4 ― 2011/02/14 22:49
記憶だけで検討していた、『四角の中の五角』であるが、オリジナルの確認をしていなかったことに気がついた。『彫刻家 堀内正和の世界展 図録』(2003年11月)で確認したところ、オリジナルは近似を使っているようだった。
写真を読み取ると、正三角形の面に、各辺を八等分した斜めの格子が描かれていて、切断面がその格子点に基づいているようなのである。つまり、黄金比φ=(1+√5)/2=1.618..ではなく、8/5=1.6、5/3=1.66..という値を使っている。
(2)五面体
正四面体には正方形の切断面があり、立方体(正六面体)には正六角形の切断面がある。そして、五つの面を持つ立体・四角錐には正五角形の切断面がある。このことから浮かぶ問いは、もうひとつの五面体である三角柱(五面体はグラフ的には2種しかない)からも正五角形の面が切り出せるだろうか、というものだ。しかし、残念ながら、これはできないのであった(きちんと証明はしていないけれど)。
(3)無理数の近似における「7」
(1)に関連した話である。無理数の近似といえば、次のようなものがある。精度にばらつきはあるが、みな7を使っているのがクールだ。
√2 ≒ 7/5 ≒ 10/7
√3 ≒ 7/4 ≒ 12/7
自然対数の底 e ≒19/7
円周率π≒ 22/7
√2≒7/5や、√3≒7/4は、折り紙で使ったこともある。使う機会はあまりなさそうだが、上の式から得られる e≒1+√3と、π≒√2+√3いった式も、ちょっと面白い。
いっぽう、黄金比φには、7を使ったよい近似がない。黄金比の近似は、フィボナッチ数列の2項の比で表せるが、この数列に7はない。(フィボナッチ数列:1,1から始めて、2項の和を次の項にする:1,1,2,3,5,8,13,..)
√5ならば、φ≒5/3から、√5≒7/3と、「7がらみ」の式も得られるが、これはちょっと精度が低い。










最近のコメント