第28回折り紙の科学・数学・教育研究集会など ― 2020/07/15 00:00
7月18日(土) 10:00-17:00に、日本折紙学会主催、第28回折り紙の科学・数学・教育研究集会をオンラインで行います。チケット販売中です(コンビニ決済もあります)。
ひとつ前に書いた、斉藤茂吉の随筆『紙幣鶴』の鶴はどういうものだったのか、という話のつづきである。これを読んだ知人が、「1920年ごろのオーストリアの1000クローネを調べたら、いま一般的な紙幣とは長方形の比率がずいぶん違っていました」と教えてくれた。たしかに、かなり横が短い。古銭ショップの映像から計測すると、100対151であった。これなら、折り返して、鶴を折りやすそうだ。
アマビコ、アマビエなどの図像が、感染症避けの護符として注目を集めているが、よりメジャーなのは、鍾馗や元三大師(がんざんだいし)だ。元三大師こと、平安時代の高僧・良源の伝説を起源とする護符は、角大師(つのだいし)と豆大師の二種類がある。角大師は西洋の悪魔に似た図像で、豆大師は、観音信仰に基づく三十三体の小さな大師像を描いたものだ。

月刊『みすず』など ― 2020/07/04 22:44
先週、美術大学のリモート講義で、非常勤講師をした。講義のアウトラインは、折り紙造形における黄金比の話とした。講義の準備で「ゴールデン・ボックス」という黄金比を使った作品をあらためて検討しているうちに、山折りと谷折りを変えるだけで、薔薇のような模様ができることに気がついた。組むのはパズルだが、面白い。

タイガースファンは、プロ野球が始まってむしろストレスが増えたと言っているらしい。しかし、無観客ゲームで練習のような感覚もあり、まあこんなものかと、思いの外ストレスは低い。ただし、パ・リーグ最下位のバファローズの勝ち星の数は気になって、「今日のオリックスくんはどうかなあ」とチェックをしている。

たのしみは常に見なれぬ鳥の来て軒遠からぬ樹に鳴きし時
たのしみは人も訪(と)ひこず事もなく心をいれて書(ふみ)を見る時

かはるがはる蜂吐き出して釣鐘草 島村元



ブックデザインなど ― 2020/06/21 10:18
『宇宙と素粒子』(千夜千冊エディション)(松岡正剛)の装幀に、作品を提供した。

折り紙による幾何の問題を思いついた。自分で考えたいひとのために、解答は「シール」で隠しておく。


先日、眼鏡が破損してつくりかえたが、今度は、スマートフォンの画面に盛大にひびがはいった。木製の床の上に1mぐらいの高さから落下し、それほど強い衝撃ではなかったと思うのだが、条件が重なったためか、みごとなひびになった。

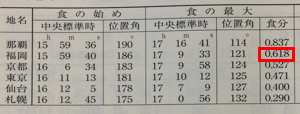
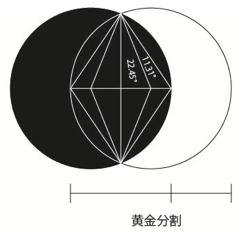
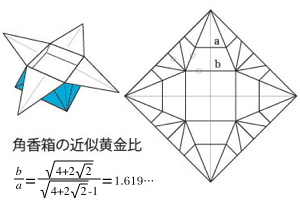
日食と角香箱 ― 2020/06/16 21:54

展開図、眼鏡、気球、サリンジャー、そして『しししし』 ― 2020/06/14 14:02





菫程小さき人に生まれたし ― 2020/05/30 21:14
「超立体」という商標のマスクは、超立方体(四次元正八胞体)とは関係はなく、ふたつの錐面の接続である。



オレンジ色が目立つ小鳥がいて、ヤマガラにしては鮮やかだなと思ったが、黒い羽の白いワンポイントなどから、ジョウビタキ(♂)であることがわかった。図鑑によると、夏にはロシア方面に渡る、いわゆる冬鳥のはずなのだが、鳴き声からも間違いなくジョウビタキである。火打石に似る鳴き声からヒタキ(火焚き)と名づけられたという説もあるようだが、バードコールの「キッ」という摩擦音が一番近い。昨年まではこの声を聞いた記憶がなく、なぜ冬鳥が夏にいるのか、帰りそこねた『幸福な王子』の逆バージョンかと心配したのだが、この10年、北に帰らずに留鳥となり繁殖している観察例が多いそうで、研究者や日本野鳥の会も注目しているらしい。














最近のコメント