いずれも卵形を描けるが、じっさいの卵とこれらの式に合理的な結びつきがあるわけではない。また、図を描く場合は、多項式の陰関数より、媒介変数をつかって(x,y)=...のかたちしたほうが扱いやすい。
極座標の媒介変数をつかった(単位)円の式は(x,y)=(sinθ,cosθ) θ=0...2π である。
このy軸のcosθに工夫をすれば、卵形が描ける。まず思いつくのはa^φbcosφとすることだ。しかし、こうすると、半周を描いてそれを反転させる必要があり、また、卵の底がわずかに凹んでしまう。卵の特徴は、どの面も凸で、かつ曲率がなめらかに変化していることである。
そこで、いろいろ考えて、次の式にした。
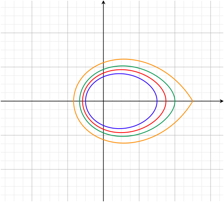
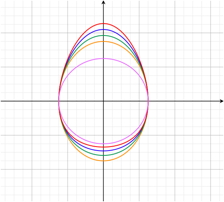
(x,y)=(sinθ,a^cosθbcosθ) θ=0...2π
指数関数の「肩の数」をcosφとしたところがミソである。これはなかなよい。
図は、b=1.4として、a=1, 1.1, 1,2, 1.3、そしてa=1, b=1(円)である。







最近のコメント